Anesthesia Pharmacology Chapter 4:  Physics and Anesthesiology: Kinetic Theory of Gases I

• ¹The approach used in this section closely follows the presentation by Dr. Richard Feynman which can be found in more complete form in the Feynman Lectures on Physics, Chapter 39.

• This section which mainly has to do with gases approaches the familiar pressure-volume and temperature relationships described earlier from a molecular or atomic point of view.  Some of the most basic relationships may be understood in terms of underlying physical characteristics using this molecular or atomic approach.  

  • For example, equal volumes of gases assuming the same pressure in temperature will contain the same number of molecules.  

  • Whereas this appears to be readily accepted as fact, the question is whether or not this conclusion can be obtained from basic Newton's laws.

• As noted before, the gas laws themselves can be used without regard to the underlying mechanics or processes and the thermodynamical calculations can be made.  However, in order to get a better intuitive appreciation for these pressure-volume-temperature relationships we will consider them in terms of their underlying physical bases.

• From the earlier section and our own experiences we recognize that gases exert pressures.  We need to consider what is the cause or basis of this pressure. In the figure of the ear canal and structures below, we recognized the ear "drum".

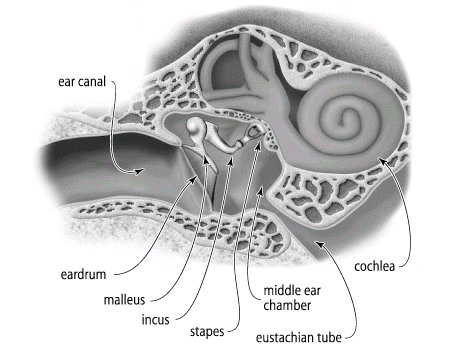
• ¹If the ear drum and associated physiological sensing and transducing structures were more sensitive than they are, we would probably hear is continual noise,  a rushing or swooshing sound due to the collision of air molecules with the ear drum.  So the  eardrum is continually under bombardment by air molecules and if the system were more sensitive all we would hear would be this background activity.  The force on the ear drum is equal on both sides, typically so the net force would be zero.  Although eardrum analogy allows us to consider or at least begin to consider the molecular basis of pressure, we might better evaluate the physical basis using a different diagram.  See below:

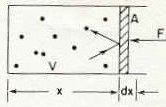
"Atoms of a gas in a box with a frictionless piston" Figure 39-1 from reference (1) below.  Page 39-3

• ¹Above we see a piston which has an area A.  

  • The volume of the box is V.  

  • The dots in the box represents individual gas molecules.  

  • The question is how much force is being exerted by the atoms in the box on the piston.  

    • As described in the figure legend above, this is a "frictionless" piston and therefore the atoms banging on one side and transferring momentum to the piston would eventually pushed the piston to the right out of the box.  

    • So we want to know how much force (F) would keep the piston from being pushed.

• ¹We will consider the force as force per unit area A.  

  • For the area A then, the force would be written as a number times the area.  

  • Pressure would be then equal to the force applied to the piston to keep it from moving divided by the area of the piston (allowing the expression to be force per unit area) or:

  • P = F / A

• ¹ To extend the idea a little further, let's consider the case in which we will move the piston a small distance represented in the figure above as dx ( x). 

  • The work done on the gas by compressing it by moving the piston the differential amount -dx is the force times the distance moved or dW.   

  • Since F = P * A (by rearranging P = F / A) then the differential work dW is equal to the pressure times the area times the distance "which is also equal to minus the pressure times the change in the volume" OR

dW = F(-dx) = -PAdx = -PdV; (Adx is the volume)

(note that area times the distance moved dx is the volume, explaining why -PAdx = -PdV; also the minus sign indicates that as we move dx we decrease the volume--also work is done on the gas in the process of compression)

• Going back to the earlier question of how much force is required to balance the momentum transfer from the atoms to the piston: 

  • The piston receives momentum as each molecule hits it (the molecules or atoms are flying around and different velocities (momentums) slamming in to the piston).  

  • So if nothing counteracts this momentum transfer, then the piston will begin sliding from left to right-to prevent this motion we must provide momentum transfer per second back into the system and the force F would be the amount of momentum per second required to prevent the piston from moving.

• Calculation of the momentum per second required to prevent movement:2 steps

  1. (1) Determine momentum delivered to the piston by one particular atom

  2. (2) Multiply that momentum by the number of collisions per second between atoms and the distant wall

   

• For this to work out, we must consider that the piston is a "perfect reflector" for the atoms-that is, the piston will not heat up.  

  • Furthermore, the gas is in a "steady condition" and given that the piston is standing still no energy is lost.  

  • Collisions of atoms with the piston wall are then perfectly elastic, particles leaving following collisions with the piston have the same energy they had before collision. Put another way, if an atom comes in with a certain speed and hits the piston it will rebound with the same speed.  Figure below: see reference 2.

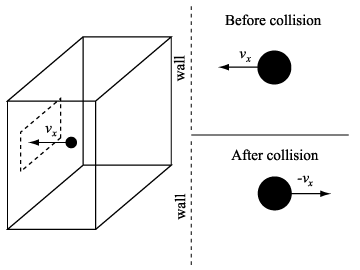
u = mv_x - ( - mv_x ) = 2mv_x
²    u is the momentum imparted to a container wall during an elastic collision. m is the mass of a molecule. v_x is the velocity in the x-direction. 

• If v is the atom's  velocity and v_x is x-component of v, and then mv_x is the x-component of the momentum "in" to the piston [recall that mass (m) times velocity = momentum].  

  • Now we have an equal amount of momentum "out" following collision with the piston indicating that the total momentum delivered to the piston by the atom in one collision is 2 mv_x because it is "'reflected'".  

  • This relationship ( 2 mv_x ) satisfies the first step required to calculate momentum delivered to the piston by one particular atom.

   

  • The next thing we need to know would be the number of collisions made by atoms per second or in a certain amount of time which we would call dt; then we could divide by dt.  

    • Let's say there are altogether N atoms in the volume V or n =N/V in a unit volume, such as a cubic centimeter or cc.

    • If we take an arbitrary time t, it may be that not all molecules have sufficient velocity or are pointed in the right direction so that within this small amount of time the molecule will collide with the piston wall. (If the molecule starts out too far away from the piston wall, it won't get there even if it's headed in the right direction before time runs out, i.e. dt).  

    • Therefore, only those molecules within the distance v_x t will hit the piston within the specified time, t.  (i.e, those that can get to the piston in time t)

    • Furthermore, the volume occupied by just those atoms which are going to hit the piston would be  v_x t A. 

      • And the number of atoms that will hit the piston is that volume times the number of atoms in a unit volume or nv_x t A.  (atoms/cc² *  number of atoms in the volume that will hit the piston  gives the number of atoms hitting the piston)

      • We need to make only one final change which is that we don't want to know the number of hits in a time t, but rather the number of hits per second so we divided by the time t, finding that the number of atoms hitting the piston per second is nv_x  A.

  • To get the total force we need only multiply the momentum delivered by one atom colliding with the piston, 2 mv_x times the number of hits/sec or nv_x  A or F = nv_x  A * 2 mv_x . 

    •  Remember that F= PA and now substituting PA for F in the preceding equation we have PA = nv_x  A * 2 mv_x and now multiplying both sides of this equation by 1 / A we have P= 2nmv² _x .This last equation indicates the relationship between pressure and the number, mass and velocities of gas molecules.

• In the development of the equation,  P= 2nmv² _x we specified that we were looking at the velocity of one particular molecule.  

  • However, the velocity of this molecule might be greater than or less than an average velocity if we were to consider all the molecules.  

  • Accordingly, the equation must be modified to specify that we want the v_x  squared term to reflect averaging over all molecules.  Accordingly we have, P= nm<v² _x > in which the brackets indicate the average. 

  •  Also note that we have dropped the 2 from the equation because we only want to consider the atoms which are moving towards the piston.  This is the same as using the average of all v_x  values multiplied by one-half.

• Another refinement is required to accommodate the fact that the molecules don't all have to be moving in the x direction, that is, <v² _x > refers to the average motion of atoms in one direction.  Since there is no constraint on which way the atoms move, <v² _x > = <v² _y > =  <v² _z >and furthermore  <v² _x > = 1/3 <v² _x + v² _y + v² _z > = <v²>/3 .  Note that the form of the equation no longer requires us to consider specific directions or vectors.

• We can also rewrite P= nm<v² _x >  as P= nm <v²>/3  or P = 2/3 n<mv²/2>

• In this form, P = 2/3 n<mv²/2>, the <mv²/2> is the kinetic energy of the molecule.  

• Also, recall that n = N/V since N/V is the number of atoms in each unit volume.

  • Suppose N = 1000 and V = 2cc, then N/V = 500 molecules/cc = n where n is the number of atoms per unit volume, i.e. per cc.

  • Substituting N/V for n in P = 2/3 n<mv²/2> gives P = 2/3 N/V<mv²/2> or PV = N(2/3)<mv²/2> . (We did this last set to get volume, V, into the relationship.

  •  Therefore, the pressure of the gas may be calculated if we know the molecular speeds!

   

• If we consider the case in which all the gas molecules are single atoms and disregarding any possible internal atom motion, then for this monatomic gas the kinetic energy of the center-of-mass motion accounts for all the energy.

  • The internal energy is defined as U and since the kinetic energy accounts for all the energy then the total energy U must be equal to the number of atoms in the gas times the average kinetic energy of each.

  • Note that the <mv²/2> part of the equation PV = N(2/3)<mv²/2> represents the kinetic energy and therefore we can substitute U  for N<mv²/2> giving us PV = (2/3)U .

  • To make this equation more generalizable, it is typically written PV = ( - 1)U. 

    • For example of a monatomic gas in which  (- 1) must equal 2/3,  is set to 5/3 so (5/3 - 1 = 2/3)

• When a gas is compressed, the work is represented as -PdV. 

  • If the compression is performed such that no heat energy is added or removed then all the work would be reflected in a change in internal energy U so PdV = -dU.  Also, since U = PV/ ( -1), dU = (PdV + VdP) / ( -1). 

  • Following further simplification, it can be shown that PV= C (a constant).  In circumstances (adiabatic) such that the temperature rises with compression (no heat loss to the outside), then the pressure times the volume to the 5/3 power is a constant.

    • This relationship has been derived from basic Newtonian mechanics and has been tested experimentally. 

    • This equation actually represents accurately the way monoatomic gases behave.

• ¹ The Feynman Lectures on Physics, Mainly Mechanics, Radiation and Heat by Richard P. Feynman, Robert B. Leighton and Matthew Sands, Chapter 39, Addison-Wesley Publishing Group, Palo Alto California, Chapter 39, pp. 39-2- 39-12., 1963.

• ² Keelin Chan, Physics for the Masses (...of A Level Students) http://www.jcphysics.com/