 |
 |
Anesthesia Pharmacology Chapter 4: Anesthesia Fundamentals
|
|
|
|
*(question attribution, Ira Rampil, M.D., 1995) |
"We live submerged at the bottom of an ocean of air - Torricelli, 1644"
Definitions:
Pressure = force/area
2Units:
Pascal (Pa): 1 Pa = 1 Newton/m2 or 1N/m2
atmosphere (atm): one atm =101325 Pa = 14.7 lbs/in2
bar: 1 bar = 100000 Pascal
torr: 760 torr = 1 atm
mm Hg: 1 mm Hg = 1 torr
Major properties associated with gas: pressure, volume, moles, and temperature. Equations relating pressure, volume, temperature, and moles for gas would be called an equation of state. The major properties of gases are described by the relationship PV=nRT where R is the gas constant.
|
|
|
Consider the lift pump above. Galileo was first to recognize or more correctly record that a lift pump could only raise water is high as 10.4 m or 34 ft.
The explanation was provided by Torricelli who suggested that water was being forced up the pipe as a consequence of the pressure exerted by the atmosphere on the surface of the water at the bottom of the pump.
Carrying this idea further, since mercury (Hg) is about 14 times as dense as water, Torricelli predicted that atmospheric pressure would support a column of mercury only 1/14 as high as the maximum water column. See calculations below (reference 4).
|
|
|
|
4The figure above illustrates the Torricellian tube which preceded today's barometer.
The glass tube is closed at one end, filled completely with mercury, and then inverted into a bowl of mercury.
As you know, the column of mercury will drop and it continues to drop until it reaches the height of about 760 mm above the lower surface.
The pressure the atmosphere exerted on the mercury surface in the bowl is equal to the pressure due to the weight of the mercury in the tube.
This condition is obtained at equilibrium.
A vacuum exists at the top end of the tube and this vacuum has been designated the Torricellian vacuum.
Continuing along this line of thinking, consider the following.
The weight of the mercury in the tube above is defined by its density * the volume *the acceleration.
Density is represented by the symbol
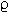(rho).
Weight =
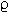*hA * g where h is
the height and A is the cross-sectional area of the mercury
column.
To obtain the equilibrium condition, this downward force must be balanced by an upward force that is equal.
This upward force comes from the atmospheric pressure which acts down on the mercury in the bowl and is transmitted equally to all parts of the fluid, in accord with Pascal's principle.
Accordingly, the upward force on the bottom of the tube is, F = PA, where P is the atmospheric pressure.
The condition of equilibrium requires that the two forces are equal, therefore:
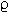*hA * g = PA
and simplifying this expression we have P =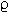
*h * g.
Acceleration due to gravity is 9.81 m/s2, the density of mercury is 13.6 x 103 kg/m3, and the height as we have noted above, is760 mm or 0.760 m. [the expression 13.6 x 103 kg/m3 utilizes "scientific notation" and corresponds to 13.6 multiplied by 1000, which is represented as103 ; therefore, the expression 13.6 x 103 is exactly equal to 13,600.]
Using the values and substituting in the equation, P =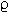
*h * g, we obtain P = 13.6 x 103 kg/m3 *
9.81 m/s2 * 0.076m OR 101 x 103N/m2
= 1.01 x 105 Pa.
This value, 1.01 x 105 Pa, corresponds atmospheric pressure. 1 atm is defined as the pressure exerted by the earth's atmosphere at sea level ( the value to more significant figures is 1.01425 x 105N/m2).
"The Newton is the Standard International Unit of force.
In physics and engineering documentation, the term newton(s) is usually abbreviated N.
One newton is the force required to cause a mass of one kilogram to accelerate at a rate of one meter per second squared in the absence of other force-producing effects.
In general, force (F) in newtons, mass (m) in kilograms, and acceleration (a) in meters per second squared are related by a formula well known in physics: F = ma"5
Before we speak specifically about application of gases in the context of anesthesia, we will first consider a number of preliminary aspects having to do with the physics of gases, including the kinetic theory of gases.
Mostly we will be concerned with interrelationships of three parameters:
(1) pressure
(2) volume and
(3) temperature.
We will begin by considering pressure which in terms of dimensions would be force per area. (P = F/A)
The standard international (SI) unit of pressure is the Pascal (Pa). In turn, 1 Pa = 1 Newton/meter2. (a meter will be abbreviated as m)
From our earlier definition in which pressure equals force / area, the Newton must be a measure of force.
In fact, the Newton is defined as a unit of force which is required to accelerate a mass of 1 kg 1 m per second per second.
Also note that the force of gravity acting on a mass will give that mass an acceleration of 9.8 m/s2.
If the mass is 1 kg then the force of gravity on that mass would be 9.8 Newtons.
Therefore, 1 Pa = 1 Newton/m2 = kg/m s2. [simplified from (1kg 1m/s2)/m2]
Sometimes we discuss gas pressure in terms of different units, i.e. other than Pascal units.
For example, we may wish to describe gas pressure in terms of "atmospheres" or mm Hg.
The relationship between one atmosphere and Pa units is: 1 atmosphere (1 atm) = 1.013 x 105 Pa
To determine the relationship between atm and mm Hg, we first specify a standard temperature of 25oC, the density of mercury is 13.6 g/cm3 (water is defined as having a density of 1 g/cm3) and that the acceleration due to gravity is 9.8 m/s2.
We now need to determine, using mercury as the fluid, how tall a column of mercury would be supported by a pressure of 1 atmosphere?
To resolve this question we need to recognize that there is a formal relationship between an applied pressure (P) and the height of a fluid.
This relationship is:
P = dgh where "d" is the density of the fluid (a temperature-dependent value), "g" is the acceleration to gravity and "h" would be the height of the column in, for example, cm. Again using the density of mercury as 13.6 g/cm3 we obtain the following taking care to appreciate the units of dimension of the quantities. For consistency of units note that we represent Pa as kg/m s2
hHg = P/dHgg which is a rearrangement of the above equation P = dgh, so
hHg = P/dHgg = [(1 atm) (1.013 x 105 Pa/atm) (kg/Pa m s2)] / [(13.6 g/cm3) (106 cm3/1 m3) (1 kg/1000g) (9.8 m/s2)] OR
hHg = 0.76 m = 76 cm = 760 mm Hg
The above derivation is adapted from that of Professor Larry Gladney, Ph.D. Dept of Physics, University of Pennsylvania
|
|
|
|
|
|
Let's begin this discussion by noting the equation P = F/A showing the relationship between force, area and pressure.
To use a familiar example, we will consider to syringes of different sizes as shown below:
The force exerted by the thumb on the plunger will be considered to be the same in both cases.
If the applied force is the same in both cases, then the pressure will be determined in a manner dependent on the inverse of the area, P = F/A.
The area of the smaller syringe plunger surface is A and the area of the larger syringe plunger surface is 4A.
If the smaller syringe were a 2 ml syringe, then the plunger surface area would be about 5 x 10-5 m2 with the area of the larger syringe (say a 20 mls syringe) would be about 2.5 x 10-4 m2 . Figure above: (©) University of Kansas)
Consider the case in which the force applied by the thumb is set at 25 Newtons: then substituting into our equation P = F/A we have 25 Newtons / 5 x 10-5 m2 which is 500 kPa (kiloPascals).
Since the area is greater for the 20 ml syringe we can calculate a new pressure, i.e. 25 Newtons / 2.5 x 10-4 m2 or 100 kPa. [100kPa is approximately 1 atm].
Now 1 atm is about 760 mm Hg which is about 100 kPa.
This means that if we take systolic blood pressure as 120 mm Hg (16 kPa), then our 100 kPa (1 atm) is about 6 times this systolic blood pressure.
To better appreciate some of these pressures, let's consider the following clinical correlation.
In a type of regional anesthesia (Bier block), local anesthetic is injected intravenously and the local anesthetic concentration is maintained by pressure cuff which is inflated to above the systolic pressure.
The clinical advantage of this procedure is that systemic toxicity associated with local anesthetics, particularly CNS toxicity is less likely to occur.
1In the diagram above (©) University of Kansas) note there are two forces to consider.
The first force is applied to inflate the pressure cuff (F, in blue), whereas a second force (F, in red) is applied to the syringe plunger.
From our calculations above using
the 20 ml syringe example is possible to apply sufficient plunger force to
cause pressures well in excess of usual systolic blood pressures.
Accordingly, if excessive pressure is applied to the syringe plunger the local anesthetic can enter the vascular system distal to the cuff at a pressure sufficient to overcome the "cuff" barrier and as a consequence, the drug can gain access to the systemic circulation.
1Another clinical correlation example in which the relationship between pressure, area, and force are highlighted would be that of bedsore formation.
In one example, if the patient weight over a localized region (10-2m2) [which is equal to 10 cm x 10 cm] is set at 20 kg, then the force over this area can be found by applying the relationship F = ma (force = mass times acceleration) which is Newton's second law.
Acceleration is due to gravity and is set at 9.8 m/s2 with the mass being 20 kg in our example; therefore, the force = 20 kg x 9.8m/s2 = 196 Newtons.
Now we can apply our equation P = F/A where P is the pressure and F is the force with A representing area; 196 N/10-2m2 = 19.6 kPa.
The final step required to understand the clinical consequence is to compare the pressure exerted on this region (19.6 kPa) with a systolic blood pressure of 120 mmHg or about 16 kPa.
Therefore the pressure exerted
on the region is sufficient to cut off blood supply, thus promoting
bedsore development at the pressure point.
|
|
Clinical Correlation
Peripheral Nerve Blocks:
6The Bier block is frequently referred to as intravenous regional anesthesia and is most commonly performed on the upper extremity for hand or forearm surgery of limited duration. In order to ensure reliability, safety, and expectable patient satisfaction, certain steps are required.
A small-gauge intravenous cannula is placed in the dorsum of the hand vein, away from the surgical site, and distally. The needle size will be about a 20-gauge needle.
A double tourniquet would be secured around the upper arm (not all centers may use the double tourniquet method, although it is the standard approach) -- see below
|
|
|
|
The arm is exsanguinated by wrapping with a wide elastic band (esmarch).
The approach might utilize a 10 cm Webril padding band.
A pneumatic double cuff is placed and the proximal tourniquet inflated.
The lower end of the distal cuff will be secured using foam tape to prevent movement.
With the proximal cuff inflated, 40-50 mls (cc) of 0.5% lidocaine is injected through the intravenous catheter.
Subsequently (usually within minutes) anesthesia is obtained and the operation may be initiated.
Note that the distal cuff remains in place, but uninflated
When the patient begins to experience the discomfort from the effects of the proximal tourniquet, the distal cuff, under which anesthetic has been infused is inflated and that point the proximal cuff may be deflated.
Later, the distal cuff will also become painful, as a result of ischemia.
The maximal permissible time is really the maximal allowable ischemic time limit which limits the anesthesia period to about 90 minutes.
A major concern in this anesthetic method is the possibility for local anesthetic toxicity, which is a rare complication unless tourniquet time turns out to be < about 30 minutes.
In that case repetitive deflation and re-inflation of the tourniquet will tend to limit systemic local anesthetic toxicity.
Communication with the patient in the circumstances is required to detect early symptoms of toxicity, which implies that excessive sedation should be avoided.
|
|
|
3aSome Assumptions
Matter is composed of discrete particles. These particles are atoms or molecules
Ideal gases are composed of molecules or atoms that are relatively far apart compared to their own size. Gas molecules are extremely small compared to the distance between gas molecules.
For the purposes of defining an ideal gas, the gas particles can be thought of as points which have no dimension and occupy no volume.
This assumption is not helpful when one considers kinetic theory in which we want to describe gas molecular position and momentum information.
Gas particles behave in accord with classical laws of motion (Newtonian mechanics). Furthermore, this motion is random.
There are no attractive forces between gas molecules or between the molecules that make up the container surfaces and the gas molecules. Again, there will be such attraction in reality; however, for the purpose of the ideal gas law theory these interactions may be ignored.
Molecular collisions occur between molecules and between molecules and container boundaries; that is, gas molecules bang into the container sides and furthermore energy will be transferred between molecules when these collisions occur.
This comment is consistent with thinking in terms of "momentum" transfer.
Overall, energy will be conserved in these collisions.
However, a given molecule may gain energy at the expense of another molecule [the overall energy, considering all the molecules, will remain constant in accord with the conservation of energy requirement]
Energy (which may be described in terms of kinetic energy or speed) will be distributed among the molecules in a manner predicted by the Maxwell Boltzmann distribution relationship.
The average kinetic energy of all the molecules will be proportional to the absolute temperature, but for any given instant, molecules in a certain volume will not possess the exact same amount of energy and will be characterized by some distribution of speeds.
The gas laws formalize the relationships between pressure, volume, and temperature.
These interrelationships can be described without regard to the underlying mechanisms or machinery responsible.
This field of study is thermodynamics.
Later, we will consider the underlying processes that speak to the molecular or atomic detail.
3aGas Law variables:
Volume:
The volume of the gas is defined as a three-dimensional space in turn defined by container walls.
The container has no leaks.
The variable for volume is V.
Volume may be represented by differing units.
For example, liters (L) or milliliters (mL) are two such units. [A liter is a cubic decimeter (dm3) and by analogy, more familiarly, a milliliter is a cubic centimeter (cc or cm3).]
In our subsequent analysis, the volume may change in accord with a change in some other parameter.
Therefore, for those circumstances, the container "walls" may be "movable" to accommodate these volume changes.
However, in all cases a perfect seal is present such that despite volume changes molecules do not escape from the container.
Sometimes, we may wish to hold the volume constant as we for example increase the temperature.
For those cases, we would use materials in the container walls that are very resistant to the pressure and do not readily move.
We appreciate this for example in an oxygen tank, i.e. we can heat the tank up and it doesn't seem to expand very much -- at least until it blows up.
Temperature:
We will have a lot to say about temperature in order to describe it in terms of underlying kinetic, molecular processes and subsequent sections.
At present note that gases are defined by a temperature that may be measured and represented in degrees Celsius (oC).
Celsius refers to Anders Celsius, which explains at least why the word is capitalized.
Temperature is represented in terms of a symbol by T.
For our calculations, we typically will not use the Celsius scale but rather the Kelvin scale (symbol = K, no degree symbol).
All gas law problems use Kelvin temperatures. If you use Celsius degrees, the answers will be wrong.
Fortunately, it is easy to convert between Celsius and Kelvin temperatures.
Specifically, Kelvin = Celsius + 273.15 (we will use 273, forgetting about the 0.15 part).
As an example, 25oC = 25 + 273 = 298oK.
Standard temperature by definition is 0° Celsius or 273oK.
Another point which we will discuss in detail later is that the Kelvin temperature of a gas is directly proportional to its kinetic energy, meaning that, for example, tripling the Kelvin temperature corresponds to a tripling of the kinetic energy of the system
Pressure
As we shall see later, pressure is a consequence of gas molecules banging against the container walls and is defined as force/area.
Pressure units are different, depending on circumstance or whim and are as follows:
Atmospheres (atm)
Millimeters of mercury (mmHg)
Pascals (Pa) or more frequently kiloPascals( kPa)
Standard pressure is defined as 1 atm or 760.0 mmHg or 101.325 kPa. In anesthesiology, we utilize all of these designations and are able to represent pressures interchangeably
|
Atm (atmosphere) |
|
mmHg (millimeters of mercury) |
|
Torr (same as mmHg) |
|
Pa (Pascal; kPa = kiloPascal) |
|
K (Kelvin) |
|
oC = degrees Celsius |
|
K = °C + 273 |
|
1 cm3 (cubic centimeter) = 1 mL (milliliter) |
|
1 dm3 (cubic decimeter) = 1 L (liter) = 1000 mL |
|
0.00 °C = 273 K |
|
1.00 atm = 760.0 mm Hg = 101.325 kPa = 101,325 Pa |
Gas quantity
The amount of the gas can be represented by moles (mol) or in grams (g).
If grams are used, we often have to convert to moles.
The lowercase n is used to represent some variable amount of the gas in moles, recalling that our other variables are all capitalized.
Note this standard representation in the relationship PV=nRT, which says that pressure times volume equals the number of moles times the gas constant times the temperature (Kelvin).
3aPressure Conversion Examples
Convert 0.875 atm to mmHg
solution: multiply the atm value by 760.0 mmHg/atm (answer = 0.875 atm * (760.0 mmHg/atm); note that the atm units cancel out
Convert 745 mmHg to atm
solution divide the mmHg value by 760mmHg/atm (answer = 745mmHg/760.0 mmHg/atm)
Convert 0.955 atm to kPa, recalling that 1 atm = 101.325 kPa
solution: multiply the atm number by 101.325 kPa/atm (answer = 0.955 atm * 101.325 kPa/atm; here again atm units cancel, leaving kPa
Convert 98.35 kPa to atm
solution: divide the kPa value by 101.325 kPA/atm (answer = 98.35 kPA/101.325 kPa/atm)
Convert 740 mmHg to kPA, recalling that 760mmHg = 1 atm = 101.325 kPa
solution: answer = 740 mmHg * (101.325 kPa/760.0 mmHg)
Convert 99.25 kPa to mmHg
solution: answer = 99.25 kPa * (760 mmHg / 101.325 kPa)
1Boyle's Law: This is the first gas law and states that if the temperature is held constant, the volume of a given amount of gas will vary inversely with the absolute pressure.
So at constant temperature, P1 x V1 = P2 x V2. For example, if we have a cylinder of gas under pressure equivalent to 13,800 kPa (the internal volume or capacity of the cylinder is about 10 liters), how much gas would be available at atmospheric pressure which we will say is about 100 kPa.
Substituting in the equation P1 x V1 = P2 x V2., (V2 = P1 x V1 /P2 ) we have 13,800 kPa x 10 liters) / 100 kPa = 1380 liters. Note that the internal volume of the cylinder remains of course at 10 liters so that one would really have 1370 liters available at atmospheric pressure.
Simply by plugging in numbers we can get the answer without regard for the underlying molecular processes. We'll soon see that thinking about these relationships in terms of the underlying processes may provide for a more intuitive appreciation.
|
Variables allowed to change |
Variables held constant |
Resulting relationship |
Formal designation |
|
pressure and volume |
number of molecules and temperature |
P1V1 = P2V2 |
Boyle's Law |
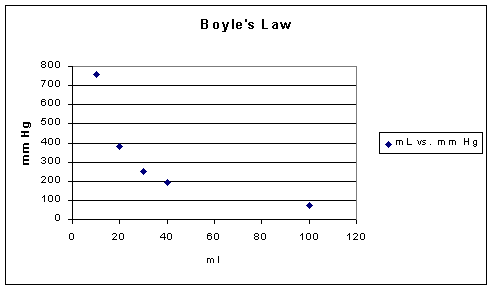
If one were to look at Boyle's Law in terms of what experiment would reveal the basic relationship, we would be comparing gas volumes to pressure with everything else held constant, e.g. temperature. The following data might be obtained:
|
Volume (ml) |
Pressure (Torr) |
PV (ml*Torr) |
|
10 |
760.0 |
7.60 x 103 |
|
20 |
379.6 |
7.59 x 103 |
|
30 |
253.2 |
7.60 x 103 |
|
40 |
191.0 |
7.64 x 103 |
From the data above the volume is inversely proportional to the pressure, recalling that everything else that might influence is held constant.
Since pressure may be defined in terms of the frequency of molecular collisions which result in momentum transfer, reducing the volume while retaining the same number of molecules increases the number of molecular collisions and therefore from the kinetic theory of gases point of view the pressure must increase
|
|
3aExamples:
2.00 L of a gas at 740 mmHg pressure. What will its volume be at standard pressure?
First recall that Boyle's Law states: P1V1 = P2V2 and in this example the starting pressure is 740 mmHg and the starting volume is 2 L.
Solution: (740.0 mmHg) * (2.00 L) = (760.0 mmHg) * x, where x is the symbol for the unknown.
The answer = (740.0 mmHg * 2.00 L) / 760.0 mmHg.
We need to recall here that standard conditions for pressure is 760 mmHg.
5.00 L of a gas is at 1.08 atm.
Supposing the volume was 10.0 L, what would be the pressure?
Solution: same approach as above, P1V1 = P2V2 , or [1.08 atm * 5.00 L] = x * 10.0 L; x = (1.08 atm * 5.00 L) / 10.0 L; note that the volume unit (L) cancel, leaving the pressure unit, atm.
Here is another problem which references the figure below:
|
|
In this example the cylinder has a cross-sectional area of 0.04m2 and a height of 0.2m (left cylinder).
There are no leaks between the piston and the cylinder walls and therefore movement of the piston can cause compression of the gas.
At the beginning the air is at atmospheric pressure and fills the cylinder (atmospheric pressure = 1.01 x 105 N/m2).
Suppose that the piston is pushed until it is within 0.12m of the top of the cylinder.
The question is what would be the new pressure of the air. In accord with Boyle's law, we mandate that the gas temperature remains constant and that we don't have to take into account the small volume of the gas in the gas gauge itself.
As always we start with the basic Boyle's law statement, which defines the initial and final system states by the subscripts 1 & 2: P1V1 = P2V2 .
Since we are interested in the final pressure, we can rearrange the relationship as follows P2= P1V1 / V2 and now plugging in the numbers.
P2 = (1.01 x 105 N/m2)(0.20 m x 0.040 m2) /(0.12m x 0.040 m2) = 1.7 x 105N/m2 which is the new pressure and can also be written 1.7 x 105Pa.
In this example, we were not directly provided the volume; however, if we know the cross-sectional area, which we did, we can multiply that by the height and get the volume.
This approach can be visualized as essentially getting the volume of a stack of CDs if one knows the cross-sectional area of one CD and multiplies by the number of CDs for the given height.
|
|
|
Since we're going to talk about Charles's law next, we begin by noting that in a way it was discovered by Joseph Louis Gay-Lussac, in 1802 but in that published work he noted that there had been some earlier but unpublished work done by Jacque Charles.
Charles found that oxygen, nitrogen, hydrogen, carbon dioxide, and air all expanded to the same extent over an 80 degree interval.
With that in mind, the picture below is that of Charles. On exam, we will not require you to know which is which.
As elaborated below, Charles's law illustrates the relationship between volume and temperature if pressure and the amount of the gas are held constant.
|
Variables allowed to change |
Variables held constant |
Resulting relationship |
Formal designation |
|
volume and temperature |
number of molecules and pressure |
V1/T1=V2/T2 |
Charles' Law |
1Charles' Law a.k.a. Gay Lussac's Law: This is the second gas law which states that at constant pressure, the volume of a gas will vary directly with the absolute temperature.
So here we have volume is proportional to temperature or V / T = constant.
Therefore, at constant pressure if we double the temperature (given in degrees Kelvin, i.e. oC + 273) we double the volume.
In an approach similar to the one employed above for Boyle's Law, the experiment that reveals Charles's Law would be performed such that all pressure and the number of molecules are held constant, the relationship between volume in temperature can be examined. The following data might be obtained:
|
ml |
Temperature (oC) |
Temperature (oK) |
ml/oK |
|
40.0 |
0.0 |
273.2 |
0.146 |
|
44.0 |
25.0 |
298.2 |
0.148 |
|
47.7 |
50.0 |
323.2 |
0.148 |
|
51.3 |
75.0 |
348.2 |
0.147 |
|
55.3 |
100.0 |
373.2 |
0.148 |
|
80.0 |
273.2 |
546.3 |
0.146 |
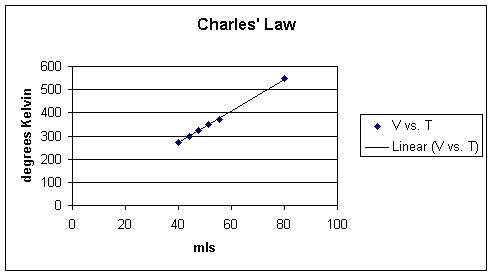
As noted above, if the volume increases then the temperature increases and similarly if the volume decreases than the temperature will also decrease.
Up to this point we haven't consider temperature in terms of molecular motion, but we will, and for the moment must suppose the we already have.
So let's suppose that the temperature is increased.
This statement is the same as saying that the gas molecules will have a higher velocity and will tend impact the walls of the container more often.
A very temporary increase in pressure will occur and this change will cause the container walls to expand.
But we said the pressure was constant, so what happened?
When the container walls expanded, that meant that molecules had to go further in distance to reach the walls and therefore in any given instant there would be a reduced number of collisions compared to the case before volume expansion.
A reduction in the number of collision translates to a reduction in pressure back to the initial state.
Now this pressure increase, although real, last for a very, very short period of time.
The flip side is also true.
That is, suppose the container walls were moved such of the volume would be rapidly increased.
The pressure (defined in terms of number of molecular collisions with the container walls) would decrease since the molecules now have to travel farther to impact the walls.
However, since pressure must remain constant in this model, the only way to get enough molecules to the wall to support the increased volume is to increase the temperature (reflected in more rapid motion of the molecules) thereby getting molecules to the walls more rapidly (overcoming the longer distance and keeping pressure constant)
3aThe equation is represented not only as V / T = constant (k), but probably more usefully as V1/T1 = V2T2 or in accord with the graphic below which illustrates two methods for representing the equation mathematically.
3aRemember, always use degrees Kelvin for temperature representation.
|
|
3aExamples
Problem: a gas is collected and found to fill a volume of 2.85 L at 25°C. What will the volume be at standard temperature?
Solution: firstly, convert 25°C to degrees Kelvin, giving 298°K. Remember that standard temperature is 273°K. The equation looks as follows: answer = (2.85 L/298°K) = x / 273°K
Problem: 4.4L of the gas is collected at 50°C. Now what would be volume become if the system was cooled to 25°C?
Solution: if you are inclined to just divided 4.4L by 2 because the temperature is being halved, you would be wrong -- not having converted to°K first. Don't make this mistake on the exam. Instead we convert the temperatures to degrees Kelvin and then use the relationship in the above graphic or in particular (4.40 L/323 °K) = x /298°K
Problem: 5.0 L of the gas is collected at 100°K and then the gas is permitted to expand to 20 L. What would be the new temperature that would be required in order to maintain the same pressure in accord with Charles's law?
solution: (5.0 L/100°K) = 20 L / x
The third gas law indicates that at constant volume the absolute pressure on the gas varies directly with the absolute temperature or P / T = constant. Therefore at constant volume a doubling of temperature results in a doubling of pressure
Ideal Gas Law
3aThe ideal gas law was described first by Clapeyron (above). The derivation of this law follows from statements of the six gas laws, represented in the following way:
PV = k1
V / T = k2
P / T = k3
V / n = k4
P / n = k5
1 / nT = 1 / k6
3aThe k values in the above expressions and different subscripts, indicating different values; however, multiplying all these terms together results in the following expression: P3V3 / n3T3 = k1k2k3k4k5 / k6 .
Taking the cube root of k1k2k3k4k5 / k6 results in a constant called R.
The units for each of the k values are k1 = atm-L; k2 = L/K; k3 = atm/K; k4 = L/mol; k5 = atm/mol and 1/k6 = 1/mol-oK.
The overall unit following the taking of the cube root is L-atm/mol-K (liters atmospheres per mole degree Kelvin) and taking the cube root of the expression P3V3 / n3T3 = k1k2k3k4k5 / k6 gives us this form PV /nT = R or rearranging to obtain the more common form of the equation, PV = nRT. One approach to obtain numerical value for R is as follows:
Consider we have 1.000 mole of a gas at standard temperature and pressure (STP).
One mole of a gas will have the volume of 22.414 L (in most calculations we use 22.4 L, but in this case will use the more precise value.
22.414 L represents the molar volume which is the volume of any gas at standard temperature and pressure.
Now we will substitute in the PV = nRT expression the following values-- (1.000 atm)* (22.414 L) = (1.000 mole)* (R) *(273.15 oK).
Solving for R results in the following number 0.08206 L-atm/mol-K. The value of the "gas constant" depends on units; so that representing the gas constant in terms of Joules we get 8.3145 Joules/mole-K.
For our calculations we will use the 0.08206 L-atm/mol-oK value.
3aExamples
Problem: It is observed that 2.1025 g of a gas occupies 2.85L. at 22.0°C and a pressure of 740.0 mmHg.
The question is how many moles of the gas is represented.
You are going to use the above value for the gas constant and recall that its units are L-atm/mol-oK, we now know that in our calculations we have to represent pressure in terms of atmospheres, not mmHg even though we've been provided the pressure in those units.
Accordingly, the first step is to convert 740.0 mmHg to to its atmosphere equivalent.
Solution: Convert to atm as follows (740.0 mmHg / 760.0 mmHg/atm or 0.9737 atm.
We will use this value which is given to four significant figures.
Substituting this value for pressure into the equation we obtain (0.9737 atm) (2.850L) = (n) (0.08206 L atm/mol-oK) (295.0°K) or 0.1146 mol..
Molar mass: We may wish to calculate the mole or mass which we can now do given that we know how many moles of gas are present.
The molar mass is represented as grams per mole.
Since we know the number of grams was 2.1025 g which corresponds to 0.1146 moles, the mole or mass would be 18.34g/mol.
Ideal gas Law: PV = nRT
where P is the pressure
V is the volume
n is the number of moles
By definition, a mole which is abbreviated often mol is the amount of the material whose mass in grams is numerically equal to the molecular mass of the substance.
An example: the molecular mass of oxygen gas is 32;
therefore, a mole of oxygen gas is 32 g. (Oxygen molecules are
diatomic, O2,
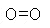,which
means that each molecule consists of two atoms, each with an atomic
mass of 16.)
Avogadro's principle, which we will consider later, indicates that a mole of any gas contains the same number of molecules, Avogadro's number which is equal to or, using scientific notation, 6.02 x 1023 molecule/mole.
6.023 x 1023 molecule/mole is the same as 6.023 followed by 23 zeros molecules/mole, a pretty big number!
The actual definition, historically, comes from carbon-12.
Carbon 12 is a common carbon isotope (carbon 14 is an example of a radioactive carbon isotope which is used in carbon-dating).
Along these lines, "4the mole is the amount of a substance of a system that contains as many elementary entities as their atoms in 0.012 kg of carbon-12." Here are some molecular masses:
Molecular hydrogen, H2, molecular mass in g/mole = 2.
Helium, He, molecular mass in g/mole = 4
Water vapor, H20, molecular mass in g/mole = 18. Note how we get the number 18 -- from the periodic table we see the atomic weight for oxygen is 16 and the atomic weight for a hydrogen atom is 1 -- therefore we add 16 + 1 + 1 = 18.
Molecular nitrogen, N2, molecular mass in g/mole = 28 -- each nitrogen atom contributes 14
Molecular oxygen: O2, molecular mass in g/mole = 32 -- each oxygen and contributes 16
Argon, Ar, molecular mass in g/mole = 40.
R is the gas constant (0.0821 L-atm/mol oK)
T is the temperature.
Inhalational
anesthetics behave in accord with the ideal gas law.
4As one could observe from the ideal gas law equation, a clear dependency on n (the number of moles) requires that increasing amount of gas by twofold, assuming constant temperature and volume, will cause an increase in pressure by twofold.
A specific example would be one in which one mole of nitrogen gas at 273.15°K and occupying a volume of 22.4 L will exhibit a pressure of 101 kPa (kilopascals).
Moreover, if we keep the volume and temperature the same but double the number of nitrogen gas moles, from 1 to 2, the pressure will then double to 202kPa.
An equation that considers concurrently a sample of matter's pressure, volume, and temperature is called an equation of state and that the quantities, pressure, volume and temperature, are state variables.
4Density: The mass, m, of a sample of matter can be considered in relation to the number of moles of the following relationship: m = n*M, where n is the number of moles and M is the gram molecular mass.
Using carbon dioxide, CO2, as an example, its gram molecular mass is Mcarbon + 2Moxygen = 12.0 + 2*(16.0)= 44.0 g/mole. We are guided by the molecular formula, CO2, which specifies one atom of carbon and two atoms of oxygen.
The density is defined by the equation
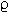=m/V = nM/(nRT/P) = MR/RT.
Using this equation and using a molecular mass of CO2 represented using the units of kg/mol results in the following:
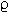= (44 x 10-3
kg/mol) * (1.01 x 105N/m2) / 8.31 J/mol-oK)* (296oK)
or 1.81 kg/m3 . For this example, we
considered the temperature to be 23°C, which explains the 296°K
value in the denominator.
| Variables allowed to change | Variables held constant | Resulting relationship | Formal designation |
| pressure and volume | number of molecules and temperature | P1V1 = P2V2 | Boyle's Law |
| volume and temperature | number of molecules and pressure | V1/T1=V2/T2 | Charles' Law |
| pressure and temperature | number of molecules and volume | P1/T1=P2/T2 | Amonton's Law |
| number molecules and volume | pressure and temperature | V1/n1=V2/n2 | Avogadro's Law |
| pressure, volume, & temperature | number of molecules | P1V1/T1=P2V2/T2 | Combined Gas Law |
| pressure, volume, temperature & number of molecules |
-- |
P1V1/n1T1=P2V2/n2T2 | Ideal Gas Law |
|
|
|
1Basic Physics and Measurement in Anaesthesia, Davis, P.D., Parbrook, G.D. and Kenny G.N.C, 4th Edition, Butterworth Heinemann, pp 2-3, 1995.
2Dr. Fred Senese, General Chemistry OnLine : http://antoine.fsu.umd.edu/chem/senese/101/gases/
3Jones, E.R. and Childers, R.L, "Gas Laws and Kinetic Theory" in Contemporary College Physics Addison-Wesley, Reading, Massachusetts, 1993, p 281.
3aPark, John L. "The Kinetic Molecular Theory of Ideal Gases, http://dbhs.wvusd.k12.ca.us/GasLaw/Basics-of-KMT.html
4Jones, E.R. and Childers, R.L, "Gas Laws and Kinetic Theory" in Contemporary College Physics Addison-Wesley, Reading, Massachusetts, 1993, p 325-346
5on-line definition, Newton: http://whatis.techtarget.com/definition/0,,sid9_gci523548,00.html
6Glenn, D.M and Angel, J.M, "Peripheral Nerve Blocks" in Anesthesia Secrets, 2nd editions, James Duke, editor, Hanley & Belfus, Philadelphia, p. 367, 2000.
7Dhother, S, "Bier Block" in Peripheral Nerve Blocks: A color atlas, Jacques E. Chelly, editor, Lippincott Williams & Wilkins, Philadelpha, pp. 121-123, 1999
