Anesthesia Pharmacology Chapter 4:  Physics and Anesthesiology

Bernoulli's equation: derivation

• This derivation which embodies concepts described earlier in the equation of continuity will he focused on the interrelationships between flow velocity and pressure. We need to be concerned with pressure, kinetic, and potential energy densities and we can  illustrate the important aspects using the two figures below⁴⁷. (adapted from reference 47)

• First focusing on the figure on the left and in particular region 1, we want to describe the amount of work needed to move to certain amount of fluid designated V along a distance of x₁.  

  • The amount of work has to take into account the amount of fluid to be transported, therefore the area, A₁, (cross-sectional area) also must be specified. 

  • The work on the input side needed to move this volume will be equal to P₁A₁x₁ .  

  • From our earlier discussions we would think of pressure in terms of kinetic energy, probably mainly translational kinetic energy and also stands to reason that the work would have to include the magnitude of the area involved as well as how far (x₁) one needed to move.  So the region 1 work is P₁A₁x₁ .

• As we look at the right side figure we see a couple of things: firstly, the tube appears to get larger so that the equal volume,V , is contained within a reduced tube length,x₂ .  As noted, the cross-sectional area is greater (A₂).  The region 2 work has the same form as before although a negative sign is placed in front of the quantity to reflect that the region 2 fluid is moving against the force caused by the pressure of the fluid to the right of region 2.  The region 2 is then -P₂A₂x₂ . Since the fluid is considered incompressible, the displaced volumes will be equal and since the volume is equal to the cross-sectional area times the distance moved we would have A₁x₁ =A₂x₂ .  The last consideration is that we're transporting the fluid up hill, against gravity, so that the work done by gravity described as follows:

  • Work done by gravity = -mg(h₂-h₁) where m is the mass which would be the volume of fluid times its density (m = A₁x₁ =A₂x₂) or V. Now substituting for mass we have the gravitational work equal to -gV(h₂-h₁). As you might guess, if we aren't moving the fluid uphill or downhill, but rather looking at a horizontal flow this term will drop out of the final equation.

• ⁴⁷We may now describe the overall work, including the gravitational work as follows

  1. W = P₁V - P₂V - gV(h₂-h₁)

  2. Recalled that we said that at the mass was equivalent to V and then furthermore there is a relationship between kinetic energy and work and that this relationship is that the change in kinetic energy equals work or KE = W.

  3. So the change in kinetic energy must be equal to the difference in the energy states describing region 1 and region 2 or [recalling that KE = 1/2 mv²]

     1. 1/2V₂ v₂² - 1/2V₁ v₁² :noting we're looking at 2  different velocities (v₁ and v₂⁾ two different masses, V₁ & V₂ .

  4. and W =1/2V₂ v₂² - 1/2V₁ v₁² = P₁V - P₂V - gV(h₂-h₁); after dividing through (cancelling) byV we have the final form for the Bernoulli equation: 

     • P₁ + gh₁ + 1/2v₁² = P₂ + gh₂ + 1/2v₂² = constant

• ⁴⁷ To simplify the case,  suppose that we have a horizontal tube  and therefore h₁₌h₂  and furthermore combining the equation of continuity [v₁ = (A₂/A₁)/v₂)]  with the Bernoulli equation we obtain:

  • P₂ = P₁ + [(v²₂ (A₂²-A₁²)) / 2A₁² ] 

    • By inspection of the equation we note that if A₁ is greater than A₂ than this term [(v²₂ (A₂²-A₁²)) / 2A₁²].on the right side of the equation will be negative. 

    • Therefore, P₂ must be less than  P₁ .  

    • Again considering the principles of conservation of energy and mass we note that the velocity of the molecules must be higher in the more constricted regions of the pipe in order to move the appropriate volume through (conservation mass) then the pressure in the constricted region compensates in the other direction and must be lower.

  • One  additional consideration is that for viscous fluids some of the work done in moving fluid is actually dissipated as a result of frictional forces in the liquid which is directly reflecting viscosity. For viscous fluids which would include water or blood  of form of the Bernoulli equation :is slightly different because of the viscosity effect and is P₂ < P₁ + [(v²₂ (A₂²-A₁²)) / 2A₁² ]. This relationship is qualitatively applicable to both gases and liquids

• An example problem that illustrates the above relationship:

  • In this problem, the objective is to determine the pressure difference (pressure change) assuming that the cross-sectional area A₁ = 15 cm² and the cross-sectional area A₂= 7.5 cm² and that v₂ =4.5 m/sec. Recalling that [v₁ = (A₂/A₁)/v₂)] we will use the relationship P = P₂ - P₁ = v₂²[(A₂²-A₁²)/2A₁²)] where = 1.0 x 10³ kg/m³ and now substituting:

    • P = 1.0 x 10³ kg/m³ * (4.5 m/sec)² [((7.5 cm²)² - (15 cm²)² ) / 2*(15 cm²)² = -7.50 x 10³ Pa - the negative sign indicates that the pressure is less in the smaller tube which is consistent with the idea that the velocity of fluid/gas moving through the smaller tube is higher.

• Venturi meter: the above relationships indicate that a knowledge of pressure associated with a particular diameter or cross-sectional area of a tube tells us something about the velocity of flow through that region. A Venturi meter is a device that can allow determination of a velocity in a narrowed region and can be graphically described as shown below:

• Using the "U" tube and the Bernoulli's equation and equation of continuity a relationship can be developed to determine the velocity of the fluid at position A in the above diagram.  The equation is v = b [(2('-gh)) / ((a² - b²))]^1/2 where is the fluid density in the pipe and ' is the fluid density in the "U" tube while h represents the height difference between the fluid on the 2 sides of the "U" and g is the gravitational acceleration constant.  Finally, a & b represent the cross-sectional areas at position A & B respectively.  By knowing the difference in height (h) the velocity v can be calculated.

• Venturi tubes are the basis for Venturi injectors which may be used in providing suction or for producing diluted gas mixtures.  The Venturi Tube is shown below:

• ⁴⁶The Venturi oxygen mask is based on the Venturi principal in that relatively rapidly moving oxygen molecules pull along (entrainment) air molecules by two processes:

  •  1.  the first process is based on the Bernoulli effect in which there is a relative reduction in pressure associated with the higher oxygen velocity 

  • 2.  and the second  involves friction between the high-speed oxygen molecules in the lower speed air molecules which has the effect of pulling air molecules into the higher speed stream.  Translational momentum transfer occurs as the air molecules increased their velocity.

  • Entrainment ratio can be calculated as a function of the entrainment flow to the driving (oxygen) flow. Entrainment ratio = (entrainment flow) / (driving flow).  If the ratio were 8:1, then 8 l/min of air would be entrained by the driving gas (oxygen) of 1 l/min.  Factors that could change the entrainment ratio include transient obstruction, including back pressure, which would ultimately change the oxygen concentration delivered.

  • Venturi Mask (oxygen molecules: blue; air molecules green (adapted from reference 46)

Turbulent Flow

• Clinical Considerations:

  • ^46,49In our earlier consideration of Reynolds numbers, increasing flow rates were associated with a potential transition from laminar to turbulent flow properties.  In general terms turbulent flow would occur under conditions in which there would be a localized velocity increase such as at an orifice  or sharp bend in a flow stream. From the theory of continuity, it is expected that an increased flow rate would occur in such regions of narrowing and in accord with an increase in the momentum component (inertial component) localized irregularities in flow (turbulence) would be induced.  

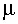  • ⁴⁹Another way of defining the Reynolds number (the ratio of momentum force to the viscous force) includes a consideration of both dynamic and kinematic fluid viscosities. R = Reynolds number = D²v²_ave / v_aveD;  in this case D is the tube diameter, v_ave is the average flow velocity, is the fluid density,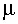is the dynamic fluid viscosity and is the kinematic fluid viscosity. 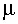Also, R = D²v²_ave / v_aveD  and R=  D v_ave / 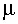and R is also  equal to  Dv_{ave /} . 

  • ⁴⁹Note that in this form: R=  D v_ave /  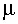 the Reynolds number is proportional to fluid density (or gas density); therefore, a reduction in density would, all other things remaining equal, reduce the Reynolds number will decrease the likelihood of turbulence.

  • ⁴⁶This effect of density on Reynolds numbers is the basis for the use of helium in combination with oxygen (heliox) in management of certain respiratory disorders because the addition of helium reduces gas density and and principal decreases the likelihood of turbulence. If turbulent flow is present, then transition to laminar flow, perhaps by using heliox, would be associated with a reduction in flow resistance which would be associated with a reduced resistance to breathing.

  • ⁵⁰Heliox: Clinical correlations

    • The use of heliox was first described over 65 years ago as a potentially effective intervention for certain types of airway obstruction⁵¹. Heliox is infrequently used for management of severe bronchospasm, probably because  of the significant efficacy of beta₂ adrenergic agonists, muscarinic agents such as ipratropium (Atrovent), and other interventions.  However, heliox has been effectively used in management is severe croup and upper airway obstruction in the pediatric patient.  The contemporary use of heliox appears limited to the mechanically ventilated critically ill pediatric patient.  The rationale for heliox use in mechanically ventilated pediatric patients who have severe bronchospasm is presumed to be related to the decrease in the Reynolds number.

  • ⁴⁶Laminar and turbulent flow in anesthesia:

• ⁴⁶The diagram above notes the critical flows for air and for an anesthetic mixture containing nitrous oxide (60%) and oxygen.  Transition between laminar and turbulent flow exhibits dependencies on gas velocity.  Furthermore gas velocity will be dependent on other factors including volume flow, tubing diameter and airway diameters.  Within the patient airway, gases tend to be more humidified and at a higher temperature, factors that reduced density.  Critical flow values then will exhibit dependencies on temperature and humidity.

• ⁴⁶The figure above indicates that the critical flow represented in l/min correlates fairly well with airway diameter (mm).  For example anesthetic flow through a 10mm internal diameter endotracheal tube would transition from laminar to turbulent flow when the flow rate would increase to above about 10 l/min.  Similarly if the tracheal diameter is about 15 mm, then the transitional flow to turbulence would occur at flow rates above about 15 l/min.  Within normal breathing cycle, higher flows, peaking at over 50 l/min. would be associated with turbulence while laminar flow would be typical elsewhere in the cycle.  The figure above indicates a greater likelihood that air flow would remain laminar compared to the combination of nitrous oxide + oxygen.

• ⁴⁶Within the respiratory tract, the narrower, smaller flow pathways in the lung, typically in the lower part of the respiratory tract, would predispose to laminar flow. For  "quiet breathing", much of the respiratory tract flow would be laminar; however speaking or coughing or sighing (deep breath) would induce turbulence.  Sharp tubing bends  and rougher(corrugated) internal surfaces also predispose to turbulence as suggested at the connecting site for an endotracheal tube (below):

• ⁴⁶Davis, P.D., Parbrook, G.D, and Kennny, G.N.C. "Fluid Flow", in Basic Physics and Measurement in Anaesthesia, 4th edition, Chapter 2, Butterworth Heinemann, Oxford, 1986. 

• ⁴⁷Jones, E.R. and Childers, R.L,  "Fluids"in Contemporary College Physics Addison-Wesley, Reading, Massachusetts, 1993, p 281.

• ⁴⁸Tom Bergson, Conservation of Mass, Glenn Research Center, NASA, http://www.grc.nasa.gov/WWW/K-12/airplane/mass.html)

• ⁴⁹Duffin, J, "Fluid Mechanics" in Physics for Anesthetists, Charles C. Thomas, Springfield, IL., 1976, 144-151.

• ⁵⁰Orsini, AJ, Stefano, JL, Leef, KH, Jasani, M, Ginn, A, Tice, L, Nadkarni, VM "Heliox improves pulmonary mechanics in a pediatric porcine model of induced severe bronchospasm and independent lung mechanical ventilation" Crit Care, 3, 65-70, 1999, ,//www.biomedcentral.com/1364-8535/3/65/

• ⁵¹Barach, A, "The use of helium in the treatment of asthma and obstructive lesions in the larynx and trachea" Ann Int Med, 9: 739-765, 1935.