Anesthesia Pharmacology Chapter 4:  Physics and Anesthesiology

 Dynamics of Inhalational Anesthesia

• Overview:  In inhalational anesthesia, the objective is to obtain a certain concentration of anesthetic molecules in the brain.  

  • This concentration of anesthetic molecules would be sufficient to cause anesthesia (independent of specific mechanisms).  

  • The actual concentration required varies depending on the anesthetic and the length of time needed to produce anesthesia is dependent on many factors including the solubility of the particular volatile agent in the blood as well as hemodynamic factors.

• ⁶Because the anesthetic is not "injected" directly into the brain, we focus our attention on the partial pressure of the agent in the lung,  recognizing that there is a rapid equilibration between the lung concentration in that observed in the brain. 

  • This rapid equilibrating process is one of the main reasons why alveolar concentrations all of anesthetic gases may be expected to reasonably describe CNS concentrations. 

    • Equilibration between the anesthetic present  in the first compartment (the lung) and subsequent compartments, e.g. blood, brain and ultimately peripheral compartments depends on several considerations:

  1. ⁶Equilibration of partial pressures is based on the inhaled agent exhibiting bidirectional flux between several compartments (lung <> blood <> CNS). 

     1. This process may be thought of at the molecular level as initially an increased probability, based on higher concentration, of an anesthetic molecule moving from the lung into the blood. 

     2. The alveolar anesthetic concentration is very high and initially the anesthetic concentration in the blood is 0. 

        1. If we were only to consider these two compartments. 

        2. Then the anesthetic concentration in the blood would increase in and turned their would be an increase in the likelihood of anesthetic molecules transferring other compartments, one of which would be back into the lung compartment. 

        3. This last process (blood to lung) would be of particular importance during the recovery, e.g. waking up phase.

  2. ⁶The speed at which an anesthetic concentration can be obtained in the CNS-the process that determines how rapidly a patient will be anesthetized-depends not only on the anesthetic concentration delivered to the alveoli but also on the relatively low capacity for the anesthetic in the blood and other tissues which must be saturated prior to significant blood to brain transfer.  

     • Accordingly, anesthetic agents which are relatively less blood soluble are associated with more rapid induction.  Recovery following discontinuation of agent administration would also be relatively faster in the case of less soluble agent.

  3. ⁶The kinetics of anesthetic transfer from the lung to the blood during induction or from the blood to the lungs during recovery tend to dominate the process. 

     1. Therefore, regulation of appropriate CNS concentrations depends on control of delivery of the drug to the lung as opposed to the depending on metabolism, for example.

• ⁶Dalton's Law: As noted earlier, the total pressure of the gas mixture is determined by the contribution of each gas separately. 

  • Each gas molecule behaves independently in the ideal case from any other gas molecule with the entire mixture behaving in accord with the ideal gas Law. 

  • Each gas will exert a partial pressure which will be proportional to its fractional "volume" or "mass". 

  • So each gas in a mixture will have its own partial pressure and the total pressure of the mixture will be the sum of each gas type's partial pressure.

• In considering the solution case, i.e. gas molecules dissolved in solution, we recognize that there are tendencies for gas molecules to move from the gas phase to the solution phase as well as from the solution phase to the gas phase. 

  • After one waits long enough, the net flux will be approximately 0 when on average the number of molecules moving from one phase to the other will be about the same. 

  • As expected, this condition defines the equilibrium state and one can note that a certain approximate number of molecules will be present in the gas phase under these conditions. 

  • Therefore, there will be a certain concentration of gas molecules in the gas phase at equilibrium and the term "tension" defines the partial pressure to the gas when it is in equilibrium.

• Given that the anesthetic gas transfers from the gas phase to the blood and the anesthetic molecules are dissolved in the blood, the number of gas molecules that dissolve will be related to a partial pressure of the (gas phase) gas that is in equilibrium with the solution as well as the solubility of the particular anesthetic gas in solution. 

  • Accordingly, for a particular anesthetic the partial pressure in solution will be dependent on two important factors the gas phase fractional volume and  the nature of the interaction of the anesthetic gas with molecules in solution. 

  • Specifically, the blood concentration of an anesthetic will depend on the gas partial pressure and blood solubility and blood solubility will be dictated by the specific physical interactions between the particular gas molecule and blood constituents, notably water molecules. 

  • Solubility of the particular gas in blood is very important since as the solubility goes up, reflecting increased dissolving capacity/cc, it may take longer before this compartment fills adequately to begin significant transfer of anesthetic molecules to other compartments such as the brain.  One might expect that  anesthetics exhibiting relatively high blood solubility might take longer to induce anesthesia because it would take longer to fill the blood reservoir (increase in blood anesthetic tension).

  • ⁶Tension and partial pressure are defined in terms of pressure units, such as mm Hg (Torr) or kPa (kilopascals). For the gas phase, as we have seen before, the fractional concentration is equal to ratio of the gas's partial pressure  to the ambient pressure, i.e. Fractional volume = P_anes/P_barometric

• ⁶Anesthetic Transfer Processes

  • In considering the process by which anesthetic gas, ultimately dissolving in blood and thereby been transported to the brain, ultimately exerts its anesthetic pharmacological property, we might begin with the gas concentration delivered to the patient. 

    • In this approach, the fresh gas outlet  (FGO) will contain volatilized anesthetic mixed with the "carrier" gas, such as oxygen.

  • Whatever the initial partial pressure would be of the gas at FGO, there will be a dilution factor to consider as this anesthetic-containing gas mixes with the volume associated with the anesthetic circuit gas, which would include the tubing, the bag, absorbent canister, and all associated piping. 

    • There will be an initial dilution with a subsequent slower climb back to the original FGO anesthetic gas concentration as the system reaches equilibrium.

  • The fractional anesthetic concentration that leaves the anesthetic circuit and enters the respiratory system is called the "fraction inspired" represented by F_I. 

  • Another important fractional anesthetic concentration is that which is present in the alveoli and is represented as F_A. 

    • As you might expect, there is a similar dilution to what we have noted earlier [FGO anesthetic gas dilution with respect to the volume of the anesthetic circuit gas] involving the dilution of the fraction inspired, F_I, by the volume presents in the airway which would include initially the trachea and bronchi and ultimately the alveolar volume itself.

  • Subsequent dilution steps occur as the anesthetic is transported across the alveolar-capillary membrane and into the pulmonary blood volume. 

    • This event marks the beginning of the increase in blood compartment gas tension of that will increasingly favor transport to the brain itself. 

    • One contemporary way of describing the tendency of anesthetic molecules to move from a region of relatively higher concentration to a region of lower concentration is to refer to a  "concentration gradient" which determines the diffusional flow direction or flux. 

    • However, we can easily consider this process in terms of just probabilities of molecules moving from regions of relatively higher concentrations to regions of lower concentrations by random motion.

  • Initial anesthetic distribution preference to the CNS results from the relatively high percentage of cardiac output received by the brain and a reasonably high tissue solubility of anesthetics in brain. 

    • Ultimately, however, distribution and redistribution will occur to other tissue compartments.

    • Therefore, although we may focus on the increase in brain concentration in the kinetics that describe that process, a process which will lead to unconsciousness, even the initially other compartments will also be concentrating anesthetic in accord with the same principles of tissue solubility and perfusion.

    • These other compartments, depending on the particular anesthetic and length of administration, following discontinuation of fresh anesthetic gas delivery, can have significant influence on the time to recovery. 

    • This effect follows from the relatively slow transfer of anesthetic from these reservoirs (e.g. fat) into the circulation which will effectively reduce the rate of decline of anesthetic CNS concentration.

  • A complete description of the partitioning of the gas between multiple compartments is relatively complex, but the principle can be illustrated by considering two compartments. 

    •   represents the partition coefficient defined as a ratio of dissolved gas in two compartments (under equilibrium conditions). 

    • The partition coefficient is an accurate representation of a ratio of solubilities (solubility represented by )of the gas in the compartments. 

    •  For example, _blood/gas = _blood/_gas = _blood/1= _blood ; _gas = 1 because for a pure gas in the gas phase must be 1.

    • Extending this argument one step further, other partition coefficients may be determined for example brain: blood (_brain/blood) which would be the volume of anesthetic in the brain divided by the volume of anesthetic in the blood or following our earlier convention, _brain/_blood .

  • Blood:gas partition coefficients for several volatile anesthetics are shown below:

• ⁶Alveolar anesthetic uptake

  • We can look at the inspired concentration of an anesthetic (F_I) compared to the alveolar fractional concentration (F_A); then, we can look at the ratio F_A/F_I and see how it varies with time as a function of several considerations, including the intrinsic anesthetic blood:gas solubility.  

    • One general conclusion might be that volatile anesthetics that have relatively low blood solubilities are associated with the most rapid rise in the F_A/F_I ratio.  

      • Before we look at this particular point we want to develop a general appreciation of the factors that influence F_I .

    • The anesthetic concentration in the gas circuit will rise in accord with first-order kinetics, described in this case by the following relationship:

      • F_I = F_FGO (1-e^-T/) where T equals time and is the time constant which in this case is the volume or capacity of the breathing circuit (V_c) divided by the fresh gas flow (FGF) [ = V_c/FGF].  

        • F_FGO is the fraction of inspired volatile agent in the gas leaving the fresh gas outlet (i.e. the vaporizer setting).

        • For example is the fresh gas flow was set at 2L/minute and the volume of the circuit was 6L than the time constant would be 3 min.  

        • With systems that obey first-order kinetics, about 95% of the theoretical maximal value will be reached following expiration of time equal to about three time constants.

      • ⁶Experimentally, the relationship between F_A and F_I is described below:

        • Ratio data from Yasuda et al: Kinetics of desflurane,  isoflurane and halothane in humans, Anesthesiology 74:489, 1991; and Yasuda, N, Lockhart, SH, Eger, EI II et al: Comparison of kinetics of sevoflurane and isoflurane in humans Anesth Analg 72: 316, 1991.

      • 

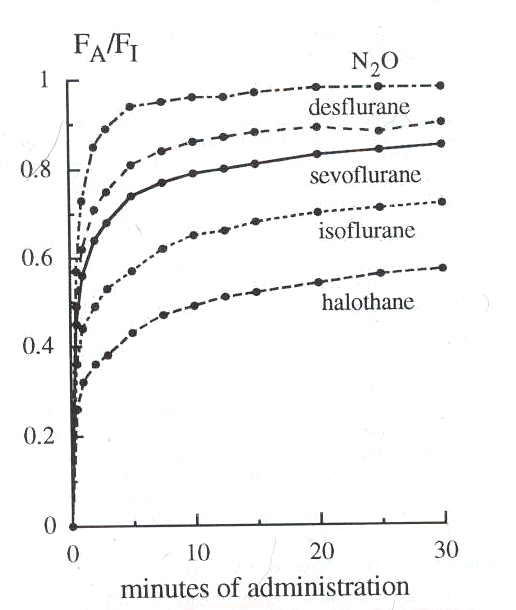
      •  Note that the least soluble agent, nitrous oxide exhibits the most rapid rate of rise

        • By contrast halothane (Fluothane) which is the highest blood: gas partition coefficient (2.5) the exhibits a very slow rate of rise.

        • First order kinetic relationships are described by a rectangular hyperbola.  The curve shape indicates the eventual attainment of  a plateau at the larger values on the x axis.  

        • With halothane (Fluothane) we see the curve still rising with quite a significant amount of time remaining before the alveolar concentration approaches that of the inspired anesthetic concentration (ratio about equal to 1)

    • Let's look at this equation F_I = F_FGO (1-e^-T/) a little more carefully and then we will look at another equation that considers how F_I is related to F_A .  

      • In the relationship F_I = F_FGO (1-e^-T/) how might we achieve a more rapid increase in  F_I ?  

      • Clearly we can alter F_FGO and .  Recall that ⁼ V_c/FGF and that V_c would be a constant, reflecting the volume of the circuit. 

        • Therefore to change , we need to change the fresh gas flow (FGF).

    • 

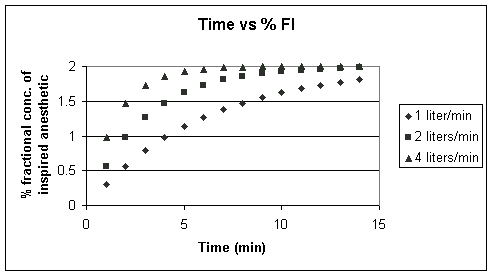
    • Above FGO is set to 2%, but the FGF is allowed to vary from 1 liter/min to 4 liters/min; Noting that ⁼ V_c/FGF  and that  V_c is a constant (6 liters), then decreases as FGF increases; changes in accord with these ratios 6 liters/1 liter/min; 6/2liters/1 liter/min; 6/4liters/1 liter/min. 

    • Note that as we increase the FGF (thereby decreasing the time constant), we more rapidly increase the F_I. Let's look at another way of doing the same thing.

    • 

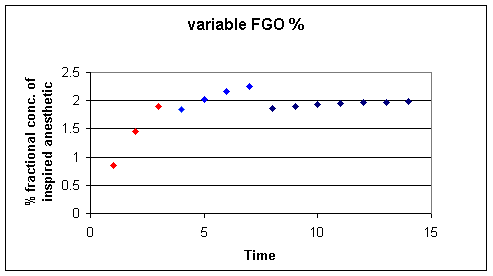
    • = 3% gas, = 2.5% gas, 2% gas; In this approach the initial gas concentration is intentionally increased above let's say a desired 2% circuit concentration.  

    • By starting with a higher gas concentration and then backing down in steps, we can more rapidly attained the desired endpoint. 

    • A similar principle will be employed to increase  induction speed and we will get to that shortly.

• ¹Basic Physics and Measurement in Anaesthesia,   Davis, P.D., Parbrook, G.D. and Kenny G.N.C, 4th Edition, Butterworth Heinemann, pp 50-51, 1995.

• ²Basic Physics and Measurement in Anaesthesia,   Davis, P.D., Parbrook, G.D. and Kenny G.N.C, 4th Edition, Butterworth Heinemann, pp 54-55, 1995.

• ³Practical Anesthesia Physics: Part 1: Airway & Vaporizer, Rampil,I., 1995  (http://anesthesia.ucsf.edu/internal/didactics/GasPhysicsHandout.pdf)

• ⁴ University of Alabama Anesthesiology Department (R. G. Ritchie, Ph.D. & P. M. Desai, M.D. (http://www.anes.uab.edu/tr97/traug19.htm)

• ⁵Pharmacology and Physiology in Anesthetic Practice, Stoelting, R.K., 3rd edition, Lippincott-Raven, Philadelphia, 1999, pp 36-37.

• ⁶Ebert, T. J. and Schmid III, P. G. "Inhalation Anesthesia" Ch. 15 in Clinical Anesthesia (Barash, P.G., Cullen, B. F., and Stoelting. R.K., eds) 4th Edition, Lippincott Williams& Wilkins, Philadelphia, pp. 377-387, 2001