|
|
|
Anesthesia Pharmacology: Physics and Anesthesiology: Kinetic Theory of Gases II
1The approach used in this section closely follows the presentation by Dr. Richard Feynman which can be found in more complete form in the Feynman Lectures on Physics, Chapter 39.
![]()
Kinetic Energy and Temperature
PV = N(2/3)<mv2/2> ,equation from the previous page, may be rewritten as V = (N(2/3)<mv2/2>) / P.
Therefore, at constant pressure, the volume would be determined by the kinetic energy, <mv2/2>, assuming no change in the number of atoms.
Kinetic energy is a property only of the "temperature".
Therefore in the case of constant pressure a change in the "temperature" would be expected to have a significant effect on the volume. This effect is represented in the movie below in which a balloon filled with the air is immersed in a beaker of liquid nitrogen, which is a temperature of 77 oK (-196oC) [Degrees Kelvin = Degrees Celsius + 273]
|
|
1Relationships between kinetic energy and temperature
1When a gas is compressed, its energy increases and it gets hotter. This section relates the idea of the gas getting hotter and temperature.
1If we consider two boxes of gas sitting right next to each other, we would recognize that eventually even if they started at different temperatures they would end up at the same temperature. We might have to wait a longtime but eventually that would be the final condition and at that point, in that condition, they would be at equal temperature. This condition represents the equilibrium state. To look at this further we consider the figure below:
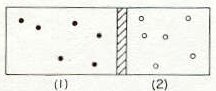
"Atoms of two different monoatomic gases separated by a movable piston" From reference 1, Figure 39-2, page 39-8.
1An example of two different monoatomic gases could be helium and argon. On the left, container 1, the atoms have mass m1 and there are n1 atoms per unit volume. Similarly, on the right, container 2, the atoms have mass m2and there are n2 atoms per unit volume. Within this framework we need to define equilibrium condition or more precisely how equilibrium state is achieved. Let's start by considering the container on the left. Atoms in the left container banging against the piston tending to move the piston to the right compressing the gas in container 2. As the pressure in container 2 builds up, the piston will be sent back to the left-this process continuing as the piston moves back and forth finally arriving at a point where the pressures appear equal on both sides.
1If the pressures are equal then the internal energies per unit volume must also be equal on each side or more particularly the number of atoms, n, times the average kinetic energies on the left side compared to the right side are equal:
n1<m1v21/2> = n2<m2v22/2>
Also, if the kinetic energies are the same i.e. <m1v21/2> = <m2v22/2>, then n1 = n2 --that is the numbers of atoms are equal. However, this latter possible equivalence remains to be shown. In this circumstance, the equivalence n1<m1v21/2> = n2<m2v22/2> follows from equal pressures, recalling that P = (2/3) n <mv2/2>
1Let's consider the way in which a system moves towards equilibrium state.
For example, n1 might be small compared to n2 but v1 large compared to v2 .
So one could have a case in which the atoms might be moving more slowly but more of them or fewer atoms hitting harder. If this is the initial condition, are we done? Is it stable?
We need to consider one additional factor and that is that the piston itself does not receive a constant, steady pressure but rather it moves back and forth in response to the intermittent banging of atoms against.
Let's say the atoms on the left are few in number. but are moving very fast. The piston gets a big impulse from the left once awhile and in moving to the right in response collides with a relatively slow atom on the right giving them more speed. [This is away of considering translational kinetic energy leading to energy transfer from a hot area to a cold area by direct collisional transfer]. So each atom can either gain or lose kinetic energy depending on which way the piston is moving when the atom hits it. This process is repeated over and over and over again until at some point the piston is moving at a particular mean square speed such that energy picked up from the atoms is occurring at about the same rate that the piston puts energy back into the atoms. Eventually when this condition is obtained, the equilibrium state has been reached.
|
1This analysis shows that if we have two different kinds of gas atoms the average kinetic energy of one is equal to the average kinetic energy of the other. (Both gases together and equilibrium in the same box). Accordingly, the heavier atoms must move more slowly than the lighter atoms in order for the equivalence to be maintained.
The mean kinetic energy is a property of the "temperature", not of the gas and accordingly then the mean kinetic energy can be used to define temperature directly.
By convention, instead of calling kinetic energy temperature a conversion factor is used between the energy of the molecule in a degree of absolute temperature call a degree Kelvin.
This constant of proportionality is k =1.38 x 10-23 joule for every degree Kelvin.
Therefore if T is the absolute temperature then being mean kinetic energy is 3/2kT, note in that in any one direction the kinetic energy is 1/2kT but since 3 independent directions are present 3*1/2kT or 3/2kT is used.
Boyle's Law revisited.
In our earlier analysis we noted that our in model the molecules don't all have to be moving in the x direction, that is, <v2 x > refers to the average motion of atoms in one direction. Since there is no constraint on which way the atoms move, <v2 x > = <v2 y > = <v2 z >and furthermore <v2 x > = 1/3 <v2 x + v2 y + v2 z > = <v2>/3 . Note that the form of the equation no longer requires us to consider specific directions.
So by extention we can rewrite P= nm<v2 x > as P= nm <v2>/3 to describe molecules moving in one direction. Finally, then by multiplying nm <v2>/3 by 2/2 we obtain P = 2/3 n<mv2/2> or P = 2/3 n<mv2/2>.
In this last form part of the expression ½ mv2 represent kinetic energy for a single molecule or, for all the atoms in each unit volume, n = N/V, so by substitution of N/V for n in P = 2/3 n<mv2/2> we obtain PV = 2/3 (Nmv2/2).
Now every element within the parenthesis constitutes the kinetic energy of the molecules or PV = 2/3 (kinetic energy) = 2/3 (constant) = a constant. Assuming constant temperature, PV = a constant is Boyles Law
Deduction of Avogadro's Hypothesis
Avogadro's hypothesis is that equal volumes of gas under the same conditions of temperature and pressure contain the same number of molecules. Is this true? Under these conditions (same conditions of temperature and pressure) p1v1 = p2v2 .
From the above relationship, we know that if p1v1 = p2v2 then P1V1 = 2/3 (N1m1v12/2) = P2V2 = 2/3 (N2m2v22/2) OR 2/3 (N1m1v12/2) = 2/3 (N2m2v22/2) [getting rid of the "2" before the parenthesis, we get (N1 ½ m1v12 )/3) =(N2 ½ m2v22) /3). Since temperature is held constant in the system, the kinetic energies per molecule must also be the same OR ½ m1v12 = ½ m2v22
Finally, dividing (N1 ½ m1v12 )/3) =(N2 ½ m2v22) /3) by ½ m1v12 = ½ m2v22 gives 1/3N1 = 1/3 N2 or N1 = N2 . This is a mathematical statement of Avogadro's hypothesis.
1 The Feynman Lectures on Physics, Mainly Mechanics, Radiation and Heat by Richard P. Feynman, Robert B. Leighton and Matthew Sands, Chapter 39, Addison-Wesley Publishing Group, Palo Alto California, Chapter 39, pp. 39-2- 39-12., 1963.
2Andrews, J.J. and Bockwell, R.C. "Delivery Systems for Inhaled Anesthetics", in Clinical Anesthesia (4/3), edited by Paul G. Barash, Bruce F. Cullen and Robert K. Stoelting, Lippincott Williams, and Wilkins, Philadelphia, p 570, 2001